Com’è definita?
La media aritmetica è certamente quella più nota e utilizzata nella statistica. È la media analitica di ordine p = 1 e potremmo definirla come il valor medio di una successione di valori 
.
Come si calcola?
Calcolare la media aritmetica, solitamente indicata con μ o , equivale a sommare tutti i valori della distribuzione (xi) e poi dividerli per la numerosità del campione N:
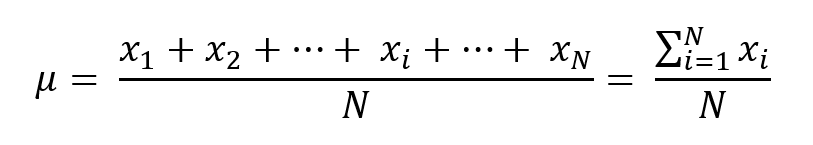
Come si applica?
Vediamo con l’esempio che segue come applicare la formula sopra descritta:
Consideriamo un campione di N=4 classi di studenti di scuola media, composte da rispettivamente: 19, 21, 25, 23 studenti. La media aritmetica si calcola come:
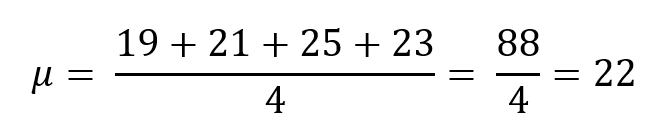
Quali proprietà la caratterizzano?
- è INTERNA, in quanto è sempre un valore intermedio tra il minimo e il massimo dei valori della distribuzione:
- Identità di somma (o proprietà di invarianza rispetto alla somma):
- Annullamento della somma algebrica degli scarti dalla media, i quali sono le differenze tra i singoli valori e la media:
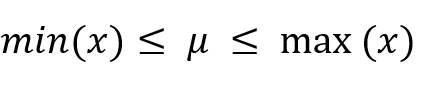
N.B: l’uguaglianza si verifica quando tutti i termini della distribuzione sono uguali.
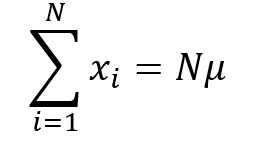
l’ammontare totale del carattere è uguale a N volte la media.
Per dimostrare questa proprietà è sufficiente considerare la definizione stessa di media aritmetica e invertire la formula, mettendo in evidenza la sommatoria.
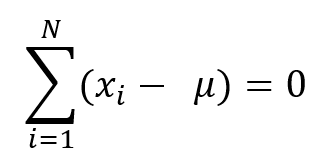
In altre parole, gli scarti positivi si compensano con quelli negativi dando luogo a un risultato nullo.
4. Minimi quadrati:
è il valore che minimizza la somma dei quadrati degli scarti e, pertanto, quello che meglio sintetizza le informazioni fornite dai dati a disposizione.
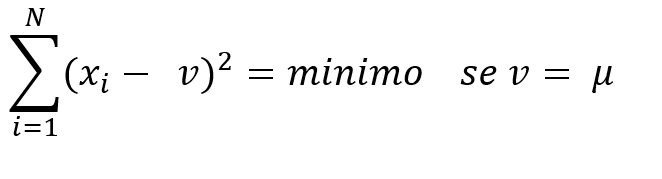
5. Equivarianza rispetto a trasformazioni lineari:
se trasformiamo i valori 
tramite la funzione 
la media aritmetica 
dei valori trasformati è connessa alla media 
dei valori originari dalla trasformazione stessa, in quanto 
.
6. Associatività:
Se abbiamo a disposizione G gruppi disgiunti, con numerosità e medie aritmetiche diverse, la media aritmetica totale si calcola “ponderando” la media di ogni gruppo per il peso dato dalla sua numerosità:
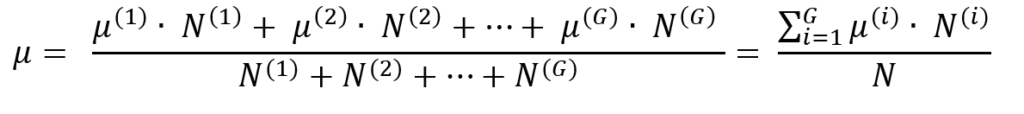
Adesso proviamo ad applicare le proprietà viste sopra per verificarle nel nostro caso:
- Internalità: la media, 22, è maggiore del minimo 19 e minore del massimo 25.
- Identità di somma: il prodotto 4 * 22 = 88 equivale alla somma dei valori 19 + 21 + 25 + 23 = 88.
- Annullamento della somma algebrica degli scarti dalla media:
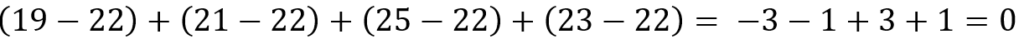
4. Minimi quadrati: la somma dei quadrati degli scarti dalla media è
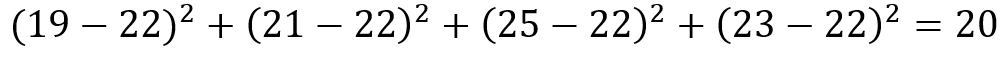
Invece se ad esempio v = 24 otteniamo:
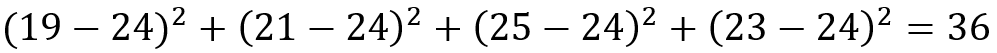
5. Equivarianza rispetto a trasformazioni lineari:
se applichiamo la trasformazione 
ai valori originari abbiamo 
La nuova media aritmetica è quindi 1 e si può ottenere applicando la trasformazione alla media aritmetica originaria (22):
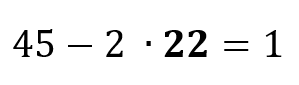
6. Se raggruppiamo i valori originari in questo modo: {19} e {21, 25, 23} per cui la media del primo gruppo è 19 mentre quella del secondo è 23, la media aritmetica totale può essere calcolata come
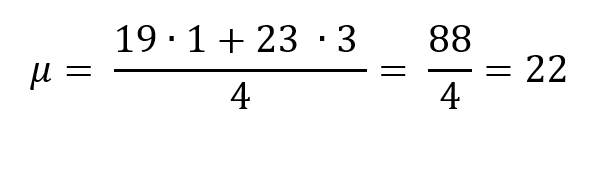
Articolo scritto in collaborazione con Marta Iacolino