Perché è utile?
La media quadratica fornisce una misura della dispersione dei dati rispetto alla media aritmetica. In particolare, essa indica quanto la deviazione dei singoli dati dalla media aritmetica è influenzata dalla loro grandezza. In altre parole, valori molto grandi o molto piccoli, essendo elevati al quadrato, avranno un’incidenza maggiore nella media quadratica rispetto ai valori intermedi. Questo la rende particolarmente utile in ambiti come la fisica o l’ingegneria, dove spesso si lavora con dati che possono assumere valori sia positivi che negativi. La media analitica di ordine 2 corrisponde alla media quadratica.
Come si calcola?
La media quadratica, che indicheremo con ![]() , di una distribuzione
, di una distribuzione ![]() di valori (xi), si calcola come radice quadrata della media aritmetica dei loro quadrati:
di valori (xi), si calcola come radice quadrata della media aritmetica dei loro quadrati:
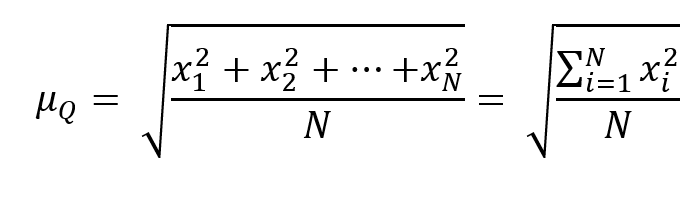
Come si applica?
Vediamo con l’esempio che segue come applicare la formula sopra esposta.
Esempio:
Ad esempio, prendiamo in considerazione le tubature italiane, le quali come è noto, sono spesso danneggiate e proviamo a stimare la quantità media di acqua fuoriuscente da N=5 di queste.
| Tubatura | xi |
| 1 | 200 |
| 2 | 150 |
| 3 | 85 |
| 4 | 420 |
| 5 | 265 |
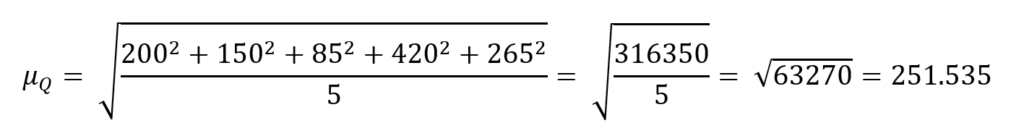
Quindi la media quadratica è 251.535 litri.
Quali proprietà la caratterizzano?
- è INTERNA, in quanto è sempre un valore intermedio tra il minimo e il massimo dei valori della distribuzione:
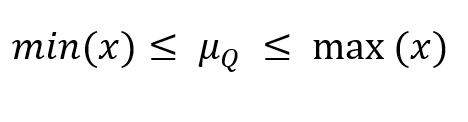
N.B: l’uguaglianza si verifica quando tutti i termini della distribuzione sono uguali.
2. Proprietà di invarianza rispetto alla somma dei quadrati:
la somma dei quadrati dei valori della distribuzione è uguale a N volte il quadrato della media quadratica.
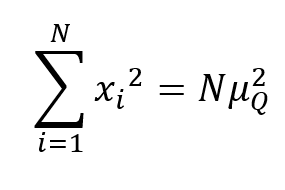
3. Omogeneità:
se tutti i valori della distribuzione sono moltiplicati per una costante c > 0, la media quadratica dei valori trasformati è c volte la media quadratica di quelli iniziali.
4. Associatività:
Se abbiamo a disposizione G gruppi disgiunti, con numerosità e medie quadratiche diverse, la media quadratica totale si calcola “ponderando” la media di ogni gruppo per il peso dato dalla sua numerosità N:
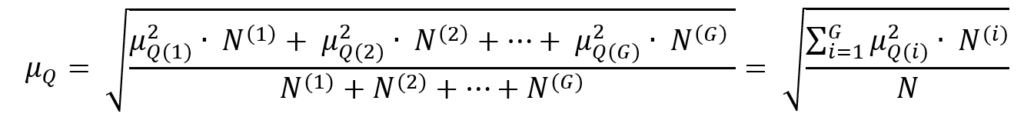
Ora applichiamo le proprietà spiegate sopra al nostro esempio:
- Internalità: la media, 251.54, è maggiore del minimo 85 e minore del massimo 420.
- Proprietà di invarianza rispetto alla somma dei quadrati:
la somma dei quadrati dei valori della distribuzione ![]() è uguale a N volte il quadrato della media quadratica
è uguale a N volte il quadrato della media quadratica ![]()
3. Omogeneità:
moltiplichiamo tutti i valori per una costante, ovvero un numero come ad esempio 4:
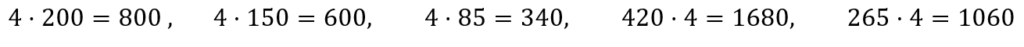
ricalcoliamo la media quadratica:
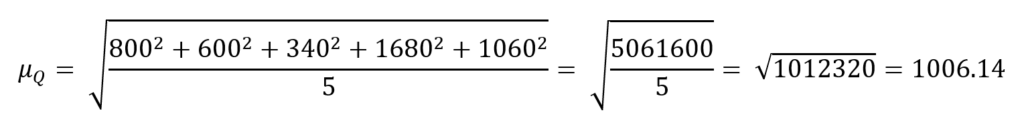
otteniamo 1006.14 litri che è esattamente 4 volte la media iniziale 251.535 litri.
- Associatività:
Supponiamo di avere 6 tubature che perdono acqua, 4 di queste perdono circa 230 litri mentre 2 perdono 125 litri. Calcoliamo la media quadratica totale:
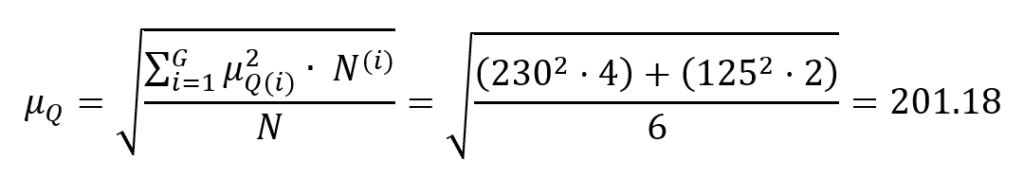
Otteniamo quindi 201.18 litri.
Articolo scritto in collaborazione con Marta Iacolino
