Cosa è la mediana?
La mediana, che indicheremo con il simbolo
, è un indice di posizione delle medie lasche che rappresenta il valore centrale di una successione ordinata, in senso crescente o decrescente, di valori. In altre parole, è il valore tale per cui prima e dopo ci siano il 50% delle osservazioni.
Quando la si utilizza?
La mediana, a differenza della media o altri indici di posizione analitiche, può essere utilizzata sia per variabili qualitative ordinabili sia per variabili quantitative, mentre non può essere calcolata per variabili qualitative sconnesse. Inoltre, non si distorce in presenza di outlier a differenza degli indici di posizione analitiche (medie).
Come la si ottiene?
Supponiamo di avere una successione statistica di valori (xi) ordinati in senso crescente 
, la posizione centrale varia a seconda che il numero totale che indichiamo con il simbolo N di valori sia pari o dispari:
- se N è DISPARI: la mediana è rappresentata dal valore che occupa la posizione
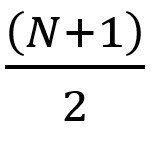e la indichiamo come 
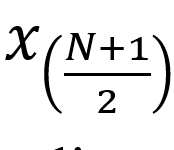. - se N è PARI: la mediana è costituita dalla media aritmetica dei valori che occupano le due posizioni centrali nella successione, ovvero le posizioni
. In particolare, la si calcola come: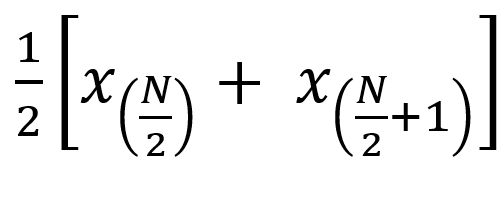 
.
Come si applica?
Vediamo con l’esempio che segue come applicare la formula sopra descritta:
Esempio: supponi di avere un insieme di dati relativi ai tempi di percorrenza di una pista di un gruppo di atleti in una gara di corsa di 200 metri. I tempi, espressi in secondi, sono i seguenti: 19.8, 21.6, 20.1, 19.5, 20.7, 21.2.
Per trovare la mediana, si ordinano i tempi in modo crescente o decrescente, ad esempio in ordine crescente: 19.5, 19.8, 20.1, 20.7, 21.2, 21.6.
Poiché il numero totale dei tempi, 6, è dispari il valore centrale si trova tra il terzo e il quarto tempo, che sono rispettivamente 20.1 e 20.7. Per trovare la mediana, si calcola la media aritmetica di questi due valori:
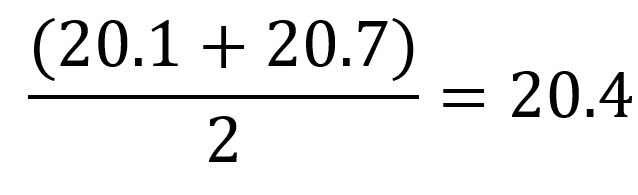
Quindi, la mediana dei tempi di questo gruppo di atleti è 20.4 secondi. Ciò significa che il 50% degli atleti hanno avuto tempi di percorrenza maggiori di 20.4 secondi e il restante 50% ha avuto tempi di percorrenza inferiore a 20.4 secondi.
Quali proprietà sono tipiche della mediana?
- è INTERNA, in quanto è sempre un valore intermedio tra il minimo e il massimo dei valori della distribuzione:
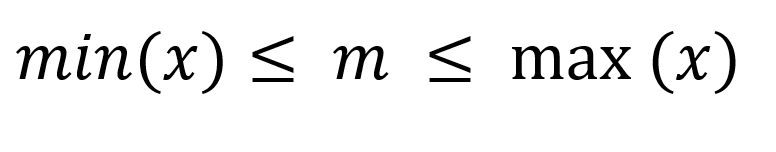
2. è il valore che minimizza la somma dei valori assoluti degli scarti:
3. Equivarianza rispetto a trasformazioni lineari:
se trasformiamo i valori 
tramite la funzione 
la mediana 
dei valori trasformati è connessa alla media 
dei valori originari dalla trasformazione stessa, in quanto 
.
Adesso proviamo ad applicare le proprietà viste sopra per verificarle nel nostro caso:
- Internalità: la mediana, 20.4, è maggiore del minimo 19.5 e minore del massimo 21.6.
2. è il valore che minimizza la somma dei valori assoluti degli scarti.
la somma dei valori assoluti degli scarti dalla mediana è
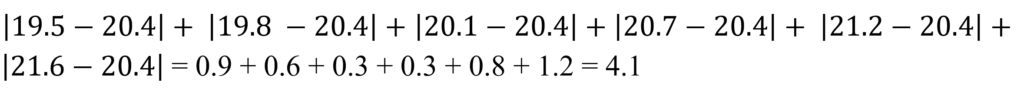
Invece se utilizziamo un altro valore come ad esempio 21.3 otteniamo:
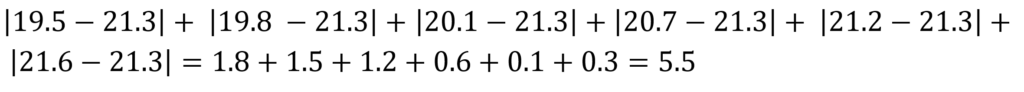
Dunque, se sottraiamo ai valori la mediana otteniamo sempre un valore più piccolo rispetto a quando sottraiamo qualsiasi altra quantità.
3. Equivarianza rispetto a trasformazioni lineari:
se applichiamo la trasformazione 
ai valori originari otteniamo:
La nuova mediana è quindi 
e si ottiene anche applicando la trasformazione alla mediana originaria (20.4):
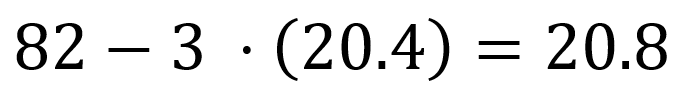
Articolo scritto in collaborazione con Marta Iacolino