Misura quanto i dati sono differenti tra loro
La varianza è una misura statistica che quantifica la dispersione di un insieme di dati rispetto alla loro media. In altre parole, indica quanto i valori di un dataset tendono a diffondersi attorno alla media aritmetica. Fa parte degli indici di dispersione.
Per comprendere in maniera semplice il concetto immaginiamo di prendere ogni giorno una strada diversa per andare a scuola e misurare ogni volta il tempo impiegato per arrivare a destinazione. Se il tempo impiegato è quasi sempre lo stesso (ad esempio 12, 13, 12, 11 minuti) allora la varianza sarà bassa, ovvero i tempi di percorrenza risultano regolari e prevedibili. Al contrario se il tempo impiegato varia maggiormente (ad esempio 15, 35, 28, 40 minuti) allora la varianza sarà alta, quindi con tempi poco prevedibili ed irregolari.
La varianza non misura quindi se arriviamo velocemente o meno (per quello bisogna tener conto del tempo medio), ma quanto è coerente il tempo di percorrenza di giorno in giorno.
Grazie all’esempio sopra possiamo capire come più la varianza sia bassa più i valori sono distribuiti in modo uniforme attorno alla media; al contrario una varianza alta è indice di una dispersione maggiore.
La varianza si calcola con la formula:
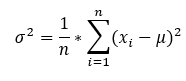
Con n che rappresenta il numero di osservazioni nel dataset, i singoli valori del dataset e
la media aritmetica del dataset.
Alcune proprietà di base della varianza sono:
- La varianza non è mai negativa, ed è 0 solo quando la variabile assume quasi certamente un valore unico;
- dato un insieme di unità statistiche, con un valore minimo ed uno massimo fra la unità, il valore massimo che può assumere la varianza è:
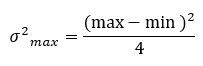
- la varianza della somma di due variabili indipendenti è uguale alla somma delle loro varianze.
La varianza è fondamentale in statistica perché serve come base per altre misure, come la deviazione standard, usata per descrivere dispersione. Aiuta inoltre a comprendere al meglio la distribuzione di probabilità di un dataset.
Articolo scritto in collaborazione con Samuele De Marzo
