Cos’è la deviazione standard?
La deviazione standard è una delle misure statistiche più utilizzate per descrivere la dispersione di un insieme di dati rispetto alla loro media. Si tratta di un valore che indica quanto i dati si discostano, in media, dal valore centrale, fornendo un’idea della variabilità o della “distribuzione” dei dati. Fa parte degli indici di disperisione.
Ha la stessa unità di misura dei dati osservati (al contrario della varianza che ha come unità di misura il quadrato dell’unità di misura dei dati) ed è la radice quadrata della varianza, la sua formula sarà infatti:
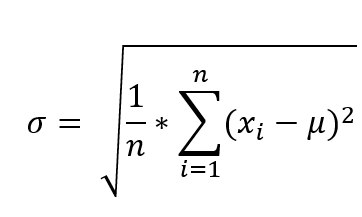
Per comprendere in maniera semplice il funzionamento di questo indice supponiamo di avere 5 mele, che hanno un peso (in grammi) di: 100, 102, 98, 101, 99; andiamo ora a vedere quanto i pesi variano rispetto alla media.
Il primo passo sarà quello di calcolare la media dei pesi delle mele, ovvero 100; passiamo poi a calcolare gli scarti rispetto alla media:
- 100 – 100 = 0;
- 102 – 100 = 2;
- 98 – 100 = -2;
- 101 – 100 = 1;
- 99 – 100 = -1.
Andiamo poi ad elevare al quadrato gli scarti ed otteniamo 0, 4, 4, 1, 1. Una volta fatto ciò si sommeranno gli scarti e si andrà a dividere per n (il numero totale di mele, 5). Per concludere si mette il risultato sotto radice e si ottiene la deviazione standard che risulta essere radice di 2 ovvero 1,41.
Questo risultato ci dice che il peso delle mele varia di circa 1,41 grammi rispetto alla media di 100 grammi.
Una deviazione standard piccola, come nel caso dell’esempio sopra, significa che i dati sono molto vicini alla media e mostrano poca dispersione; al contrario una deviazione standard elevata indica una maggiore dispersione dei dati attorno alla media.
La deviazione standard ha ampie applicazioni in varie materie, ad esempio viene usata in ambito finanziario per misurare il rischio associato ad investimenti, nella statistica descrittiva per riassumere la variabilità dei dati, nell’inferenza statistica per calcolare intervalli di confidenza e testare ipotesi, oppure in ingegneria per la valutazione di un processo produttivo.
Questo indice di dispersione risulta quindi essere uno strumento molto potente e versatile per comprendere la distribuzione dei dati, aiutando a prendere decisioni basate su una conoscenza approfondita della variabilità di ciò che si sta osservando.
Articolo scritto in collaborazione con Samuele De Marzo
