A cosa serve?
L’indice o coefficiente di concentrazione di Gini è una misura di variabilità utilizzata per descrivere la distribuzione di variabili quantitative, come reddito, voto ai partiti politici, numero di impiegati in un’azienda o numero di studenti iscritti alle varie facoltà universitarie. Ad esempio, si può usare per capire se in un determinato Paese del mondo il reddito è distribuito in modo pressoché uguale tra i cittadini o se invece è concentrato nelle mani di pochi ricchi e, dunque, vi è una forte disuguaglianza.
Quando si può usare?
Per poter misurare la concentrazione bisogna assicurarsi che le variabili a disposizione siano trasferibili, che significa che possono cedere una parte del carattere di cui dispongono senza influenzare la distribuzione dei dati o la relazione tra le variabili. Ad esempio, non sono trasferibili variabili come la statura, il peso o l’età che sono caratteristiche proprie delle persone.
Calcolo e interpretazione dell’indice di Gini:
Si calcola come:
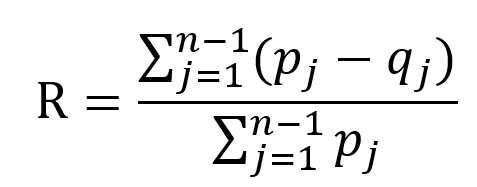
Dove:
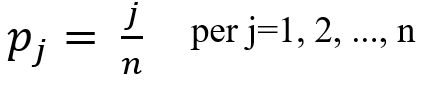
- è la frazione delle unità statistiche fino a j, dove j è un numero intero corrispondente alla posizione dell’unità una volta che le intensità (ovvero l’ammontare del carattere in ogni unità) xj sono state ordinate in modo crescente. Quindi, facendo riferimento all’esempio sulla disuguaglianza del reddito nei Paesi, se considero il secondo di 10 paesi a disposizione. pj=2/10=0,2
- è la parte del carattere posseduta delle prime j unità statistiche, si ottiene facendo un rapporto tra le intensità xj del carattere e il totale del carattere. Dunque, nell’esempio sopracitato dovrei considerare la somma cumulata del reddito dei primi due Paesi e dividere per il totale del reddito dei 10 Paesi. Ad esempio, se x1= 23000 e x2= 35000 mentre la somma dei redditi dei 10 Paesi è 450000, allora qj=(23000+35000)/45000 = 58000/45000 = 0,129
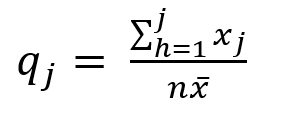
R:
Il valore di R varia tra 0 e 1 dove 0 rappresenta la situazione di assenza di concentrazione o equidistribuzione, ovvero quella in cui il carattere è distribuito in parti uguali (pari quindi alla media aritmetica) tra le diverse unità statistiche; mentre 1 rappresenta la condizione di massima concentrazione cioè quella in cui il totale del carattere è posseduto da una sola unità statistica e tutte le altre n-1 unità hanno ammontare pari a 0.
Per interpretarlo, considera che più l’indice è vicino a zero, più la concentrazione sarà bassa e quindi la distribuzione sarà più equa, mentre man mano che si avvicina a 1 la concentrazione sarà maggiore.
Esempio:
Consideriamo le iscrizioni di 650 studenti a quattro diverse facoltà universitarie e calcoliamo l’indice di concentrazione R per la distribuzione degli studenti: cerchiamo di comprendere se sono distribuiti equamente o, nel caso in cui non lo siano, in quali di queste facoltà si concentrano maggiormente e a quanto ammonta tale concentrazione. Inseriamo i dati in una tabella come quella sottostante per agevolare i calcoli:
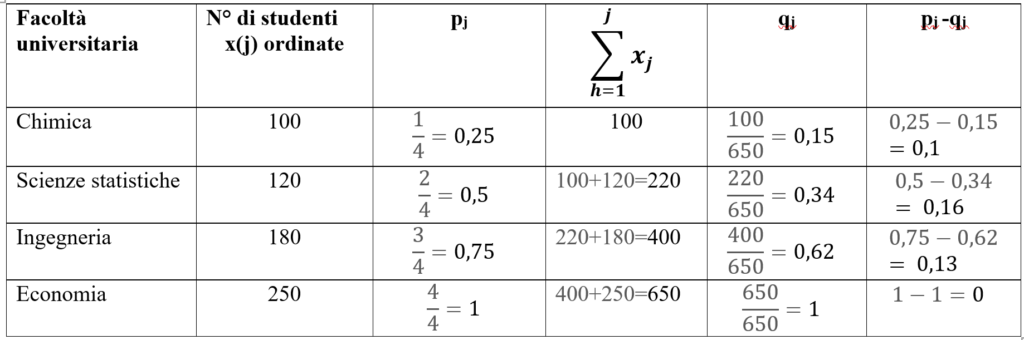
ATTENZIONE: ordiniamo le x(j), che rappresentano l’ammontare del carattere in ogni facoltà, dalla più piccola alla più grande prima di procedere con i calcoli; nel calcolo dell’indice, invece, ricordiamo di fare la sommatoria fino a n-1.
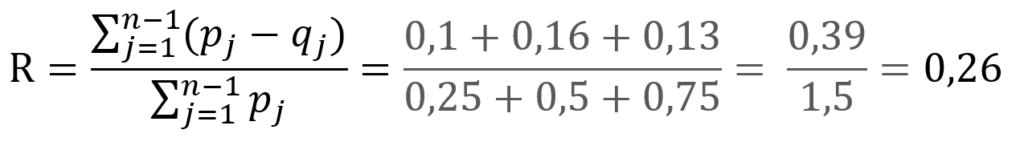
Conclusioni:
Si può dedurre che c’è concentrazione nelle iscrizioni degli studenti in una certa facoltà, quella di economia, poiché la concentrazione ottenuta è pari al 26% della massima concentrazione (nel caso in cui tutti gli studenti si iscrivessero nella stessa facoltà). Tuttavia, il livello di concentrazione è basso, ben lontano dal valore massimo, il che significa che le iscrizioni sono ripartite tra le facoltà in modo pressoché proporzionato.
Articolo scritto in collaborazione con Marta Iacolino
