Indici di posizione (medie)

Perché abbiamo bisogno di calcolare le medie? A cosa servono?

Le medie consentono di sintetizzare in un solo valore rappresentativo l’intera distribuzione di dati.

Esempio:

Ad esempio, se volessimo avere un’idea di quanto guadagnano gli impiegati di un’azienda con 20mila addetti, invece di riportare i singoli stipendi è molto più comodo ed efficace calcolarne la media, in modo da ottenere un unico valore che sintetizza lo stipendio di un addetto.

Le medie possono essere di due tipi:

  • Analitiche
  • Lasche

Medie Analitiche

Si ricavano tramite operazioni matematiche prendendo in esame tutti i valori del carattere quantitativo della distribuzione di riferimento. Questa classe di medie comprende la media aritmetica, geometrica, armonica e quadratica.

Medie Lasche

Per ottenerle si considerano solo alcuni valori particolari della distribuzione, che si trovano in determinate posizioni nella graduatoria dei valori della distribuzione. Esse comprendono il valore centrale, la moda e le medie di posizione, quali mediana e quantili. Possono essere ricavate sia per distribuzioni di caratteri quantitativi che per quelli qualitativi ma a modalità ordinabili, ad eccezione della moda che può essere determinata per qualunque tipo di carattere.

Medie analitiche di ordine p

Dato un carattere X, con modalità ,  con frequenza assoluta , la media analitica di ordine p si calcola come:

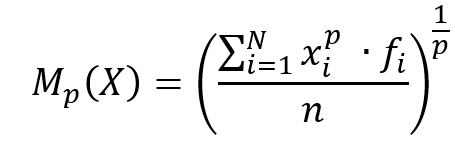
dove n è il numero totale di osservazioni.

Soddisfa la condizione di internalità di Cauchy, ovvero è compresa tra il minimo e il massimo della distribuzione:

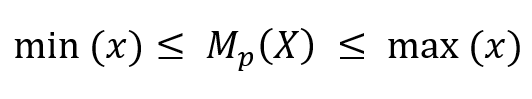
A seconda del valore di p otteniamo le varie medie analitiche:

Quali sono i criteri per definire una media analitica?

Criterio di invarianza o di Chisini:

una media analitica è definita tale se lascia invariata una certa quantità, quale ad esempio somma o prodotto. Applicando una di queste operazioni alla distribuzione originaria e a una nuova composta da M, quest’ultima costituirà una media se il risultato ottenuto nei due casi è identico. Se consideriamo la somma:

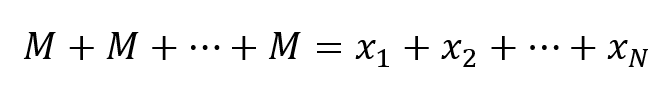
Criterio della minima perdita:

secondo questo criterio è detta media la quantità che minimizza la perdita di informazione dopo la sostituzione di M ai valori della distribuzione. La sostituzione comporta infatti un’inevitabile perdita di informazione dovuta al fatto che non si conoscono più i valori assunti dal carattere in ogni unità, ma solo il singolo valore generico della media.

Cosa significa sintetizzare una distribuzione statistica tramite una media?

Ad esempio, detta M una generica media e data una distribuzione statistica   sintetizzarla tramite una media vuol dire sostituire M a ogni osservazione  che diventa:  

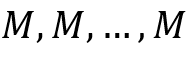
Articolo scritto in collaborazione con Marta Iacolino