Quando si utilizza ?
La media geometrica si usa quando si ha a che fare con fenomeni in progressione (come l’aumento del peso di un bambino man mano che cresce), per variazioni relative osservate nel tempo (ad esempio in giorni, mesi…) ed è utile anche per calcolare le medie in situazioni in cui le fluttuazioni dei dati sono esponenziali. La media analitica di ordine 0 corrisponde alla media geometrica.
Come si calcola?
La media geometrica, che indicheremo con 
, di una distribuzione 
di valori tutti positivi ( xi), si calcola come radice N-esima del loro prodotto:
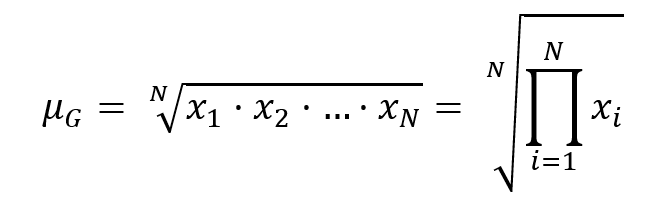
Come si applica?
Vediamo con l’esempio che segue come applicare la formula sopra esposta.
ESEMPIO:
Supponiamo di voler calcolare l’incremento medio del peso di un neonato nel corso del primo anno di vita:
| Età (in mesi) | Peso (kg) | Incrementi |
| 1 | 3.3 | |
| 2 | 4.00 | 0.7 |
| 3 | 4.6 | 0.6 |
| 4 | 5.1 | 0.5 |
| 5 | 5.5 | 0.4 |
| 6 | 6.1 | 0.6 |
| 7 | 6.6 | 0.5 |
| 8 | 7.00 | 0.4 |
| 9 | 7.5 | 0.5 |
| 10 | 8.2 | 0.7 |
| 11 | 8.95 | 0.75 |
| 12 | 9.75 | 0.8 |
Calcoliamo la media geometrica degli incrementi:
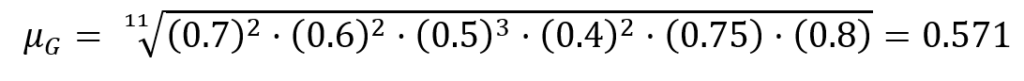
Dunque, l’incremento medio mensile è di 0.571 kg.
Quali proprietà sono tipiche della media geometrica?
- è INTERNA, in quanto è sempre un valore incluso tra il minimo e il massimo dei valori della distribuzione:
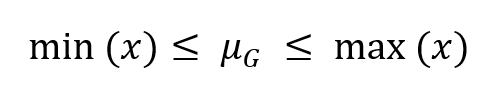
2. Identità di prodotto (o proprietà di invarianza rispetto al prodotto):
il prodotto dei valori della distribuzione è pari alla media geometrica elevata a N:
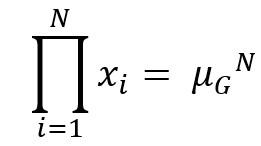
3. Omogeneità:
se tutti i valori della distribuzione sono moltiplicati per una costante c > 0, la media geometrica dei valori trasformati è c volte la media di quelli iniziali.
4. Il logaritmo della media geometrica è pari alla media aritmetica dei logaritmi dei valori della distribuzione:
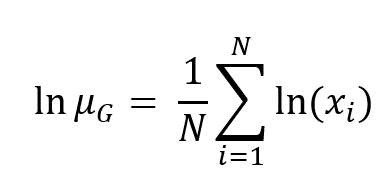
5. Associatività:
Se abbiamo a disposizione g gruppi disgiunti di un campione statistico di N unità, con numerosità 
e medie geometriche diverse 
, la media geometrica totale si calcola come:
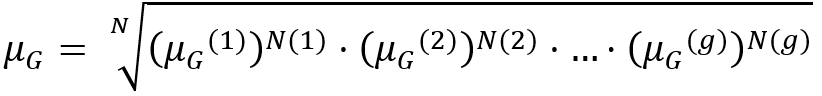
Ora proviamo ad applicare le proprietà al nostro esempio:
- Internalità: la media, 0.571, è maggiore del minimo 0.5 e minore del massimo 0.8.
- Identità di prodotto (o proprietà di invarianza rispetto al prodotto):
il prodotto dei valori della distribuzione 
è pari alla media geometrica elevata a N:
3. Omogeneità:
moltiplichiamo tutti i valori per una costante, ad esempio 2 e otteniamo
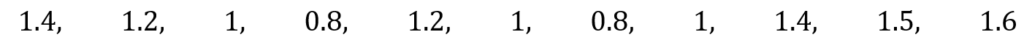
ricalcoliamo la media geometrica:
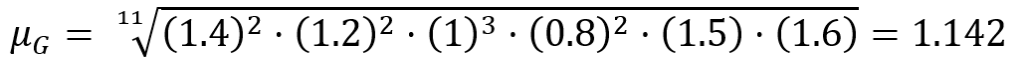
otteniamo kg che è esattamente 2 volte la media iniziale 0.571 kg.
4. Associatività:
supponiamo di voler calcolare l’incremento medio totale del peso di 6 neonati che percorrono la stessa distanza, 4 di loro hanno un incremento medio pari a 0.571 kg mentre per 2 di loro è di 0.62 kg. Calcoliamo la media geometrica totale in questo modo:
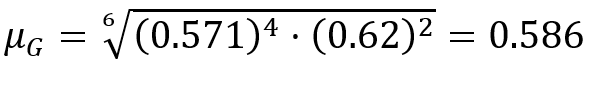
Articolo scritto in collaborazione con Marta Iacolino