Consulenze statistiche | Analisi ed interpretazione di dati
CFI è sempre compreso tra zero e 1. Si evita la sottostima di NFI e la sovrastima di NNFI.
Serve supporto professionale? Se hai bisogno di un’analisi approfondita o vuoi trasformare i tuoi dati in decisioni concrete, posso aiutarti con consulenze personalizzate. Contattami senza impegno.
📧 Email: consulenze@analisi-statistica.com
📞 Telefono: 339 5466991
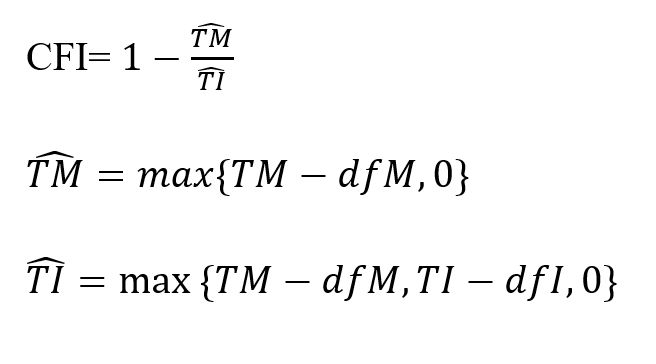
Quando la dimensione del campione non è grande, è noto che NFI ha lo svantaggio di non avvicinarsi a 1 anche se il modello corrente è corretto. NNFI corregge questo inconveniente introducendo i gradi di libertà del modello.
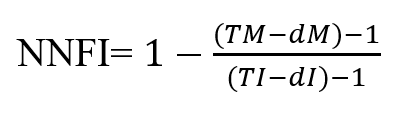
Al fine di interpretare l’indice tra 0 e 1 si effettua la trasformazione in CFI.
Serve supporto professionale? Se hai bisogno di un’analisi approfondita o vuoi trasformare i tuoi dati in decisioni concrete, posso aiutarti con consulenze personalizzate. Contattami senza impegno.
📧 Email: consulenze@analisi-statistica.com
📞 Telefono: 339 5466991
NFI valuta l’adeguatezza del modello rispetto al modello nullo che ipotizza l’assenza di relazioni tra le variabili. Siano TM e TI le statistiche del test rispettivamente nel modello corrente e nel modello di indipendenza, e siano dfM e dfI i gradi di libertà associati.
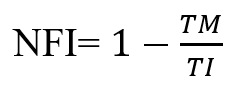
NFI varia tra 0 e 1 e un valore di NFI vicino a 1 indica un buon adattamento. Un vantaggio di questo indice è che può essere definito anche se T è solo una statistica descrittiva che non ha distribuzione nota.
Tale indice può avere problemi se il campione è piccolo. Una soluzione è utilizzare NNFI o la sua correzione CFI.
Serve supporto professionale? Se hai bisogno di un’analisi approfondita o vuoi trasformare i tuoi dati in decisioni concrete, posso aiutarti con consulenze personalizzate. Contattami senza impegno.
📧 Email: consulenze@analisi-statistica.com
📞 Telefono: 339 5466991
SRMR è una misura assoluta di adattamento ed è definita come la differenza standardizzata tra la covarianza osservata e la covarianza prevista. È una misura positivamente distorta e tale distorsione è maggiore per campioni piccoli e con pochi gradi di libertà . Poiché SRMR è una misura assoluta di adattamento, un valore pari a zero indica un adattamento perfetto. SRMR non ha penalità per la complessità del modello. Un valore inferiore a 0,08 è generalmente considerato un buon adattamento.
Serve supporto professionale? Se hai bisogno di un’analisi approfondita o vuoi trasformare i tuoi dati in decisioni concrete, posso aiutarti con consulenze personalizzate. Contattami senza impegno.
📧 Email: consulenze@analisi-statistica.com
📞 Telefono: 339 5466991
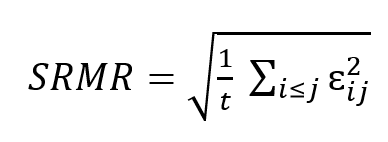
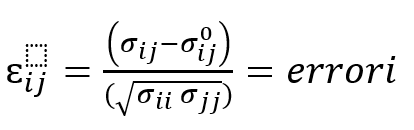
Questo software statistico è stato sviluppato appositamente per l’analisi fattoriale, sia esplorativa che confermativa e la costruzione di modelli di regressione multivariata e modelli per equazioni strutturali (Structural Equation Modeling). Lisrel è un software specifico che permette di effettuare analisi che quasi nessun altro software permette, in particolare SEM (Structural Equation Modeling). Inoltre, è rinomato e apprezzato per la facilità di interpretazione dei risultati nella parte grafica e per la possibilità di effettuare test di ipotesi successivi all’analisi (esempio: le mie domande sono valide sia per i giovani che per gli anziani).
L’analisi fattoriale confermativa si effettua attraverso l’uso di modelli di equazioni strutturali (SEM).
Leggi tutto “Analisi fattoriale confermativa”
Prima di effettuare un’analisi esplorativa dovrai scegliere la matrice di partenza. Potrai eseguire l’analisi sulla matrice di correlazioni o sulla matrice di varianze e covarianze. Se disponi del dataset potrai costruire entrambe le matrici. In passato si utilizzava solo la matrice di correlazione. Il vantaggio di tale matrice è che non crea problemi nel caso tu abbia domande con scale differenti; tuttavia essa non consente di effettuare test successivi. Inoltre dovrai effettuare dei test per verificarne la fattibilità .
Leggi tutto “Analisi fattoriale esplorativa”
L’analisi fattoriale è un insieme di tecniche statistiche utilizzate per comprendere quali siano i fattori latenti.
I fattori latenti (o variabili latenti) sono per esempio felicità , QI, sentimenti, qualità di un servizio, ovvero concetti astratti che non sono direttamente misurabili.
L’analisi fattoriale esplorativa (AFE) in cui cerchiamo le variabili latenti (es. soddisfazione, felicità , ecc.).
L’analisi fattoriale confermativa (AFC) permette di validare le ipotesi effettuate sulle relazioni tra variabili osservate e latenti, essa è quindi utilizzata quando si hanno idee abbastanza chiare su quali fattori influenzano quali variabili.
Nel seguente esempio effettueremo un’analisi fattoriale sui Big Five della personalità :
Leggi tutto “Analisi fattoriale sui Big five della personalità ”