Probabilità
Il teorema di Bayes è un concetto fondamentale nella teoria delle probabilità e nella statistica bayesiana. Esso fornisce un metodo per aggiornare le probabilità sulla base di nuove evidenze o informazioni. Il teorema è così formulato:
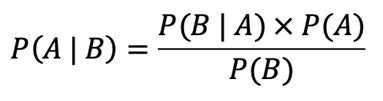
dove:
è la probabilità dell’evento A dato l’evento B (probabilità a posteriori).
è la probabilità dell’evento B dato l’evento A (probabilità di verificarsi l’evidenza B dato che l’evento A è vero).
è la probabilità dell’evento A prima di conoscere l’evidenza B (probabilità a priori).
è la probabilità dell’evidenza B (probabilità di verificarsi l’evidenza B).
Dal momento che la probabilità congiunta di A e B, ovvero la probabilità di osservare sia A che B, è uguale al prodotto delle probabilità condizionate di B dato A e della probabilità a priori di A, espressa come 
, possiamo riscrivere il teorema di Bayes in questa forma equivalente:
Il teorema di Bayes può essere applicato a una vasta gamma di problemi, consentendo di aggiornare le probabilità sulla base di nuove informazioni. È particolarmente utile quando si ha una conoscenza a priori e si desidera tenerne conto nel calcolo delle probabilità a posteriori.
Applicazione del Teorema di Bayes
Per comprendere meglio come funziona il teorema di Bayes, consideriamo un esempio pratico.
Immaginiamo di avere un test medico per una malattia rara, e vogliamo determinare la probabilità che una persona sia effettivamente malata dato il risultato positivo del test.
Definiamo gli eventi:
- A: la persona è malata.
- B: il test medico dà un risultato positivo.
Supponiamo che la malattia abbia una prevalenza del 1% nella popolazione generale, cioè P(A) = 0,01. Inoltre, assumiamo che il test abbia una sensibilità del 90% (cioè la probabilità che dia un risultato positivo quando la persona è effettivamente malata) e una specificità del 95% (cioè la probabilità che dia un risultato negativo quando la persona è effettivamente sana). Queste informazioni ci permettono di calcolare le altre probabilità coinvolte.
Utilizzando il teorema di Bayes, possiamo calcolare la probabilità che una persona sia effettivamente malata dato il risultato positivo del test:
- è la sensibilità del test, quindi la probabilità che il test medico dia un risultato positivo dato che la persona è effettivamente malata, =0,9 .
- è la prevalenza della malattia, quindi la probabilità che il test medico dia un risultato positivo prima di sapere se la persona è effettivamente malata, =0,01.
Per calcolare , dobbiamo considerare sia i casi in cui la persona è malata che i casi in cui è sana, quindi facciamo una distinzione nell’evento A:
è la probabilità che il test dia un risultato positivo quando la persona non è malata, ed è il dato complementare della specificità, quindi
è la probabilità che la persona non sia malata, quindi
Sostituendo i valori nel teorema di Bayes per calcolare la probabilità che una persona sia effettivamente malata dato il risultato positivo del test:
Quindi, dato il risultato positivo del test, la probabilità che una persona sia effettivamente malata è di circa il 15%.
Questo risultato potrebbe sembrare controintuitivo, ma è un esempio di un fenomeno noto come il ” paradosso dei falsi positivi “. Questo fenomeno avviene quando la condizione che stiamo testando (in questo caso, una malattia rara) è meno comune della probabilità di avere un falso positivo nel test.
In questo caso, la malattia ha una prevalenza molto bassa nella popolazione (1%), e il test, pur essendo abbastanza accurato, ha una probabilità del 5% di produrre un falso positivo. Di conseguenza, ci sono più falsi positivi che veri positivi: un test positivo significa solo che c’è un 15% di probabilità che la persona sia effettivamente malata.
Conclusioni
Il teorema di Bayes rappresenta uno dei pilastri portanti nella disciplina della statistica, permettendo un efficace aggiornamento delle probabilità in risposta all’acquisizione di nuovi dati. Questa capacità di calcolare le probabilità a posteriori utilizzando probabilità a priori ed evidenze emergenti lo rende indispensabile per l’analisi statistica bayesiana.
L’esempio del test medico evidenzia in maniera chiara l’applicabilità del teorema di Bayes nella vita reale. Nonostante la presenza di una malattia rara, l’utilizzo del teorema ha permesso di ottenere una stima più precisa sulla probabilità effettiva della malattia dopo un risultato positivo al test. Questo esemplifica l’importanza di considerare la prevalenza della condizione nel valutare l’efficacia di un test di screening, soprattutto quando si tratta di malattie rare.
In conclusione, il teorema di Bayes è un prezioso strumento per qualsiasi studioso o praticante di statistica, svolgendo un ruolo cruciale nella modellazione e nell’interpretazione delle probabilità, con un ampio spettro di applicabilità in numerose circostanze reali.
Articolo scritto in collaborazione con Maria Sole Chiaramonti